canvas动画包教不包会：三角函数（2）

作者：TG 日期： 2016-11-03 字数： 7199 阅读： 7689

这一章依旧是关于三角函数的，让我们来看看使用三角函数能做些什么，内容如下：

1、波形

看到下面这张邪恶的波形图，我们又要感慨一声：初中的回忆

没错，这就是正弦波，也就是正弦曲线（sin()），上面的图只是正弦函数的一个周期[0,2π]，对应正弦值范围是：[-1,1]。如果你要取sin()在[0,2π]之间的值，我们可以这样获取：

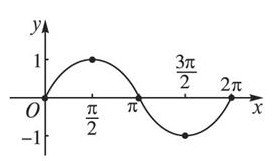
for(var angle = 0; angle < Math.PI*2; angle += 0.1){
  console.log(Math.sin(angle));
}

上面的值并没有包括-1、1和0，因为以0.1的步长是不会出现π或π/2的整数倍。

再次提醒，Math对象中所有关于三角函数的计算都是基于弧度的。

还是那句话，不要纸上谈兵，下面还是用例子说话：

（1）平滑的上下运动

在上面的例子中，我们通过 angle+=0.1 改变angle的值，然后传递给Math.sin()，它会根据angle值的变化，返回从0到1再变到-1最后回到0的值，最终就产生了跟正弦波轨迹一样的平滑运动，如下代码：

ball.x += 1;   
ball.y += Math.sin(ball.angle) * 10;   
ball.angle += 0.1;

（2）线性运动

线性运动也可称为匀速运动，也就是物体朝着一个方向做匀速（等速度）运动。对于线性运动，这里就不给例子了，你只需将上面平滑运动中的例子内这段代码注释掉就是线性运动：

ball.angle += 0.1;

（3）脉冲运动

我们都知道，动画并不仅仅局限于坐标的变化，还有很多，比如：物体颜色、物体大小等等。而脉冲运动就是通过改变物体的大小（比例）而形成的。

在这个例子中，给Ball类添加了一个scale属性，表示Ball的大小比例，通过下面的代码改变比例：

ball.scale = 1 + Math.sin(ball.angle);   
ball.angle += 0.1;   
ball.radius = 10 * ball.scale;

特别强调，不要让上面的这些例子限制了你的思维，你可以利用正弦波进行任何属性的改变，相信你会得到各种有趣酷炫的视觉效果。

2、圆周运动与椭圆运动

（1）圆周运动

圆周运动是指绕着一个完整的圆形轨迹做运动，也可以这样理解，物体离圆心的距离不变的运动。

表达式：

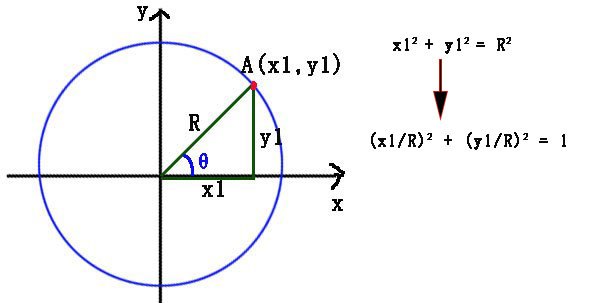
sin(θ) = x1 / R   =>   x1 = R * sin(θ)
cos(θ) = y1 / R   =>   y1 = R * cos(θ)

实例：

主要计算公式（radius为50）：

ball.x =  centerX + Math.sin(ball.angle)*radius;   
ball.y =  centerY + Math.cos(ball.angle)*radius;

（2）椭圆运动

我们将椭圆的长轴和短轴分别设为2a和2b。

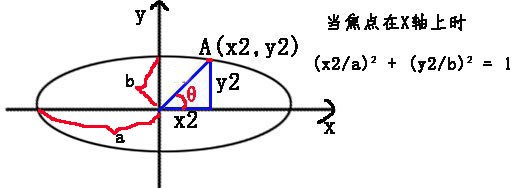
表达式：

x2 = a * cosθ
y2 = b * sinθ

椭圆和正圆的唯一区别就是，正圆上任何一个点到圆心的距离都是一样的，而椭圆却不一样。

与正圆运动不一样的是，椭圆运动是根据两个半径值来计算的（radiusX为100，radiusY为50）：

ball.x =  centerX + Math.sin(ball.angle)*radiusX;   
ball.y =  centerY + Math.cos(ball.angle)*radiusY;

3、两点间的距离（勾股定律）

很多时候，我们需要知道两个物体间的距离（对于后面的碰撞检测很重要），这时我们又要用到数学了，那就是勾股定律（要知道详情，请百度）。

假设有点A(x1,y1)和点B(x2,y2)，要求它们的距离很简单：

var dx = x2 - x1;
var dy = y2 - y1;
var dist = Math.sqrt(dx * dx + dy * dy);

dist就是两点间的距离了。其实在上面我们用到了很多，比如圆的半径，就是这样计算来的，只不过它有一个特殊点（原点(0,0)），就相等于 x1 = 0, y1 = 0 。

总结

到这里，关于三角函数的内容已经讲完了，虽然不能包含全部，但是利用这些，你能弄出很多效果（前提是你去思考）。

这两章需要各位慢慢去看，争取多动手吧！

如有错误，欢迎指正！

附录：

（1）角度与弧度互转

radians = degrees * Math.PI /180
degrees = radians * 180 / Math.PI

（2）旋转（弧度）

dx = point.x - object.x;
dy = point.y - object.y;
boject.rotation = Math.atan2(dy, dx);

（3）平滑运动

value = center + Math.sin(angle) * range;
angle += speed;

（4）圆形运动

xposition = centerX + Math.cos(angle) * radius;
yposition = centerY + Math.sin(angle) * radius;
angle += speed;

（5）椭圆运动

xposition = centerX + Math.cos(angle) * radiusX;
yposition = centerY + Math.sin(angle) * radiusY;
angle += speed;

（6）两点间的距离

var dx = x2 - x1;
var dy = y2 - y1;
var dist = Math.sqrt(dx * dx + dy * dy);