canvas动画包教不包会:速度与加速度
- 速度向量
- 加速度
- 附录:重要公式
var vx = 1; //定义x轴速度
var vy = 1; //定义y轴速度
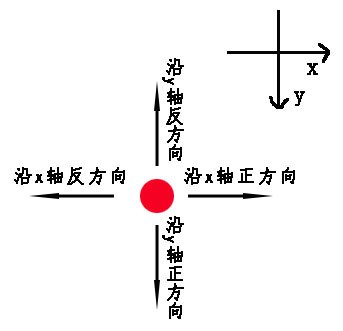
沿x轴正方向:ball.x += vx;
沿x轴反方向:ball.x -= vx;
沿y轴正方向:ball.y += vy;
沿y轴反方向:ball.y -= vy;
ball.x += ball.speed.x;
// 或
ball.y += ball.speed.y;
if(ball.x >= (canvas.width-ball.radius*2) || ball.x <= 0){
ball.speed.x = -ball.speed.x;
};
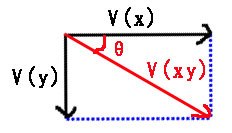
ball.x += 5;
ball.y += 4;

vx = Math.cos(45 * Math.PI / 180) *1;
vy = Math.sin(45 * Math.PI / 180)*1;

ball.speed.x += ax;
ball.x += ball.speed.x;
function keyLeft(){
ax += (-0.01);
};
function keyRight(){
ax += 0.02;
};
window.tool.captureKeyDown({"37":keyLeft,"39":keyRight}); // 这事件在用户交互一章中已封装的
2.3 重力加速度(g)
我想大家对重力加速度并不陌生,这是我们在生活中感觉最明显,比如你往上跳一跳,随后便会自然落下,这就是给你添加了一个重力加速度。
重力加速度简单来说就是y轴上的一个加速度,在计算加速度时,我们只需将重力加速度g添加到每一帧的vy(y轴上的加速度和)属性上就可以了。
我们来模拟一下重力加速度(点击按钮):
原理:小球从空中自由降落至地面,然后弹起,循环往复,直到它最终速度为零停留在地面。
代码解析:
var g = 0.3; //重力加速度
var bounce = -0.7; //反弹系数
//边界检测
if(ball.y >= (canvas.height - ball.radius * 2)) {
ball.y = canvas.height - ball.radius * 2;
ball.speed.y *= bounce; //反复相乘,最后趋近于0
};
ball.speed.y += g;
ball.y += ball.speed.y;
总结
- 速度和加速度是动画的基础元素,其中两者都是向量,包括了一个重要因素:方向。
- 要学会应用 分解 和 合成 ,将速度或加速度分解到x、y轴上,然后将每条轴上的加速度或速度相加,然后再分别与物体的位置坐标相加。
附录:
总要公式:
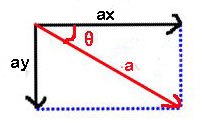
(1)将角速度分解为x、y轴上的速度向量
vx = speed * Math.cos(angle)
vy = spedd * Math.sin(angle)
(2)将角加速度分解为x、y轴上的加速度
ax = force * Math.cos(angle)
ay = force * Math.sin(angle)
(3)将加速度加入速度向量
vx += ax;
vy += ay;
(4)将速度向量加入位置坐标
object.x += vx;
object.y += vy;
下一章:边界与摩擦力

