canvas动画包教不包会:三角函数(1)
- 角度与弧度的转换
- Math对象中的三角函数
- 实例:指红针
- 波形(平滑的上下运动、线性运动、脉冲运动)
- 圆周运动与椭圆运动
- 两点间的距离(勾股定律)
1弧度 = degrees * PI / 180;
1度 = radians * 180 / PI;
1弧度 = degrees * Math.PI / 180;
1度 = radians * 180 / Math.PI;
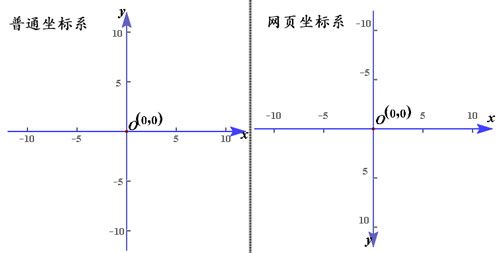
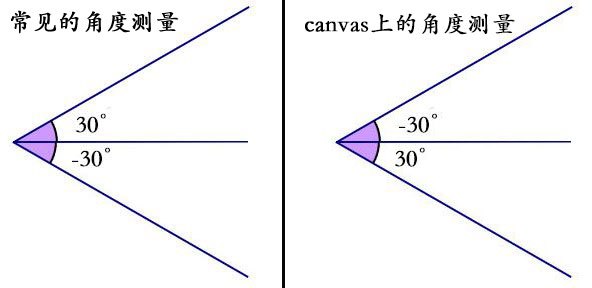
实质就是绕着X轴旋转180度后得到canvas上的坐标,角度的正负很重要。
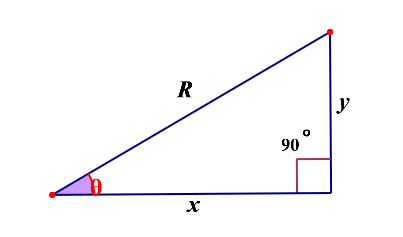
正弦:sin(θ) = y / R
余弦:cos(θ) = x / R
正切:tan(θ) = y / x
/*反三角函数*/
反正弦:arcsin(y/R) = θ
反余弦:arccos(x/R) = θ
反正切:arctan(y/x) = θ
Math.sin(θ*Math.PI/180)
Math.cos(θ*Math.PI/180)
Math.tan(θ*Math.PI/180)
/*反三角函数*/
Math.asin(y/R)*(180/Math.PI) = θ
Math.acos(x/R)*(180/Math.PI) = θ
Math.atan(y/x)*(180/Math.PI) = θ
Math.atan2(y,x)
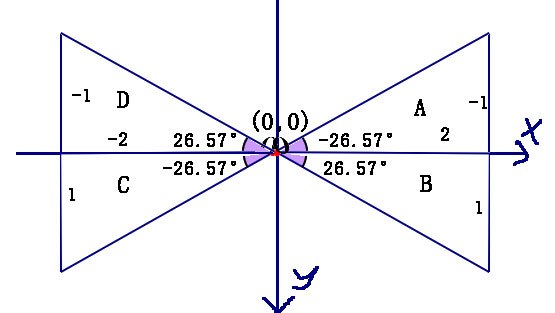
A: Math.atan(-1/2) -0.5 => Math.atan(-1/2)*180/Math.PI -26.57°
B: Math.atan(1/2) 0.5 => Math.atan(1/2)*180/Math.PI 26.57°
C: Math.atan(1/-2) -0.5 => Math.atan(1/-2)*180/Math.PI -26.57°
D: Math.atan(-1/-2) 0.5 => Math.atan(-1/-2)*180/Math.PI 26.57°
A: Math.atan2(-1,2) -0.5 => Math.atan2(-1,2)*180/Math.PI -26.57
B: Math.atan2(1,2) 0.5 => Math.atan2(1,2)*180/Math.PI 26.57
C: Math.atan2(1,-2) 2.7 => Math.atan2(1,-2)*180/Math.PI 153.43
D: Math.atan2(-1,-2) -2.7 => Math.atan2(-1,-2)*180/Math.PI -153.43
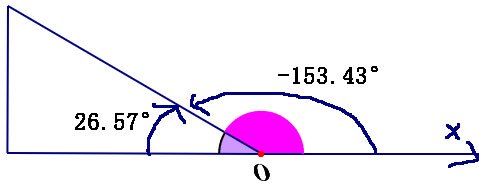
对这里例子,还是直接上图:
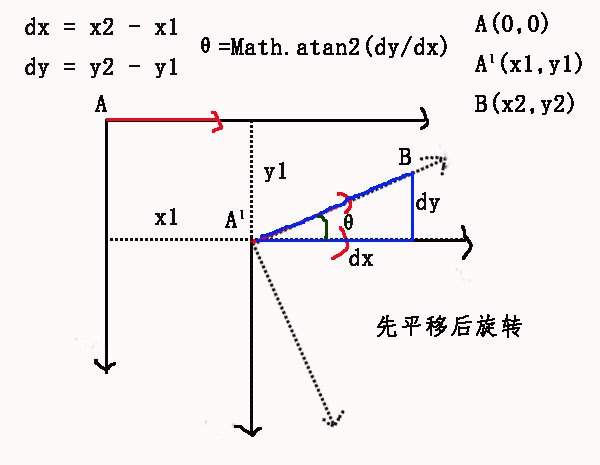
在上面的图中,红色代表了三角磁铁的指向,先平移,A1是向右平移x1,向下平移y1后的A,B是鼠标点坐标,根据鼠标坐标和三角磁铁的中心点计算出需要旋转的角度,也就是上面的θ,然后旋转cavnas。
注意:每次绘制不同的三角磁铁时,必须先使用save()保存状态,再绘制完一个三角磁铁后,再用restore()恢复上一次的状态,不然的话,每次旋转平移都会在上一次的基础上平移旋转,而不是以(0,0)点平移,后旋转了。如果不明白,可以试试不用save()和restore(),看看会发生什么。
总结
- 常用的三角函数有:Math.sin()、Math.cos()、Math.tan()
- 常用的反三角函数有:Math.asin()、Math.acos()、Math.atan()、Math.atan2()(用的频率很高)
- 一般情况下,对canvas做变形(平移、旋转、缩放等)操作时,都要使用save()和restore()来保存和恢复状态。
如有错误,欢迎指正!
下一章:《三角函数(2)》

