图解十大排序算法

本文主要讲解算法里边最经典的十大排序算法。

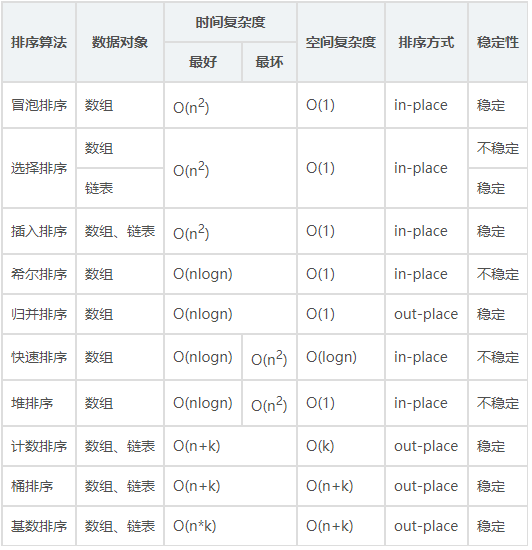
• n: 数据规模
• k:“桶”的个数
• in-place（原地排序）: 占用常数内存，不占用额外内存
• out-place: 占用额外内存

原地排序：指空间复杂度是$O(1)$的排序算法。

稳定性：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

1. 冒泡排序（Bubble Sort）

算法思想

冒泡排序是通过相邻元素之间的比较与交换，使值较小的元素逐步从后面移到前面，值较大的元素从前面移到后面，就像水底的气泡一样向上冒，故称这种排序方法为冒泡排序法。

算法步骤

• 先将数组中第 1 个元素与第 2 个元素进行比较，若前者大于后者，则两者交换位置，否则不交换；
• 然后将第 2 个元素与第 3 个元素比较，若前者大于后者，则两者交换位置，否则不交换；
• 依次重复，直到第 n - 1 个元素与第 n 个元素比较（或交换）为止。经过如此一趟排序，使得 n 个元素中值最大元素被安置在数组的第 n 个位置上；
• 接着，再对前 n - 1 个元素进行上述过程，使得前 n - 1 个元素中值最大元素被安置在第 n - 1 个位置上；
• 然后再对前 n - 2 个元素重复上述过程，直到某一趟排序过程中不出现元素交换位置的动作，排序结束。

图解思路

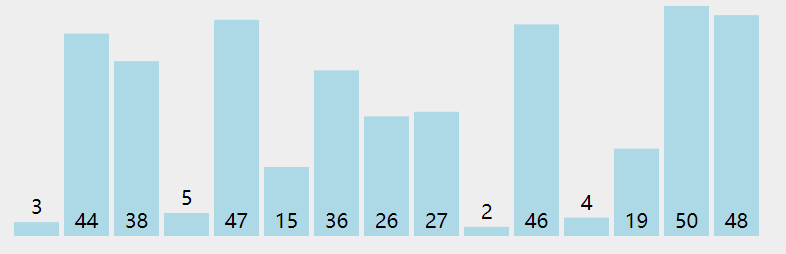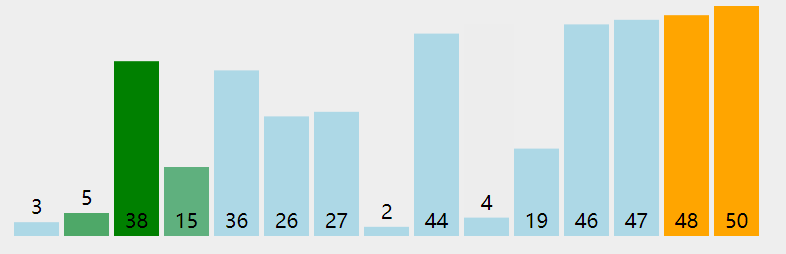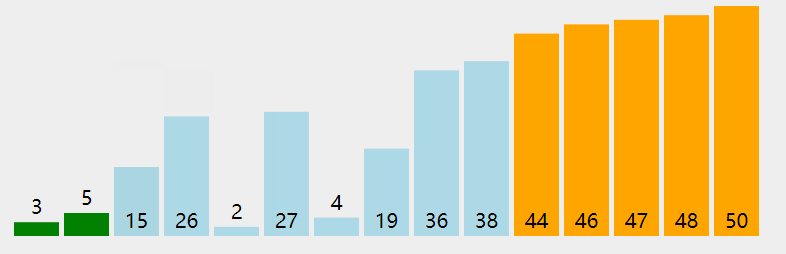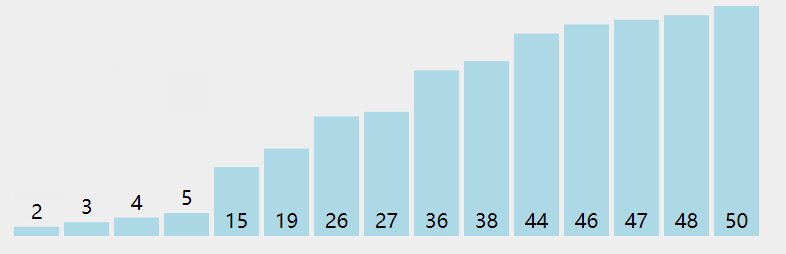
代码实现

function bubbleSort(arr) {
  const { length } = arr;
  for (let i = 0; i < length; i++) {
    // 减去i是为了不再遍历已经排序好的元素
    for (let j = 0; j < length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

复杂度分析

时间复杂度：$O(n^2)$。冒泡排序的每一轮都要遍历所有元素，总共遍历（元素数量 - 1）轮。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

2. 选择排序

算法思想

找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。

算法步骤

• 每一趟排序开始，先将 min = i （即暂时假设序列的第 i 个元素为最小值，经过比较后，再确定最小值元素的位置）。
• 第 i 趟比较结束时，这 n − i + 1 个元素中值最小的元素为下标 min 对应的元素。此时，如果 min == i，说明值最小元素就是这 n − i + 1 个元素的第 1 个元素，意味着此趟排序不必进行元素交换；否则交换第 min 个和第 i 个元素。
• 以此重复，直到最后一个元素

图解思路

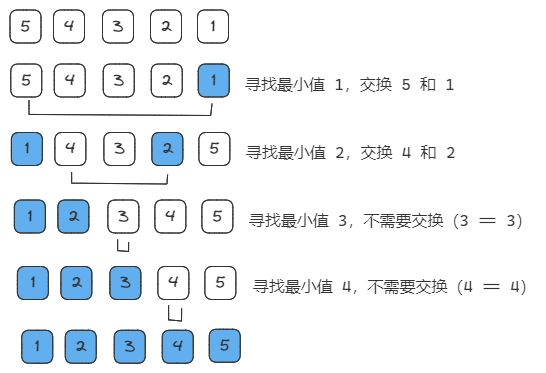
代码实现

function selectionSort(arr) {
  const { length } = arr;
  let min = 0;
  for (let i = 0; i < length - 1; i++) {
    min = i;
    for (let j = i; j < length; j++) {
      if (arr[min] > arr[j]) {
        min = j;
      } 
    }
    if (min !== i) {
      [arr[min], arr[i]] = [arr[i], arr[min]];
    }
  }
  return arr;
}

复杂度分析

时间复杂度：$O(n^2)$。对于具有 n 个元素的序列采用选择排序方法要经过 n - 1 趟排序，同时每一趟要比较的元素为 n - i + 1 个。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

3. 插入排序

算法思想

将整个序列切分为两部分：前 i - 1 个元素是有序序列，后 n - i + 1 个元素是无序序列。每一次排序，将无序序列的首元素，在有序序列中找到相应的位置并插入。

算法步骤

• 将第一个元素作为一个有序序列，将第 2 ~ n - 1 个元素作为无序序列；
• 从头至尾一次扫描无序序列，将扫描到的每个元素插入到有序序列的适当位置上。

图解思路

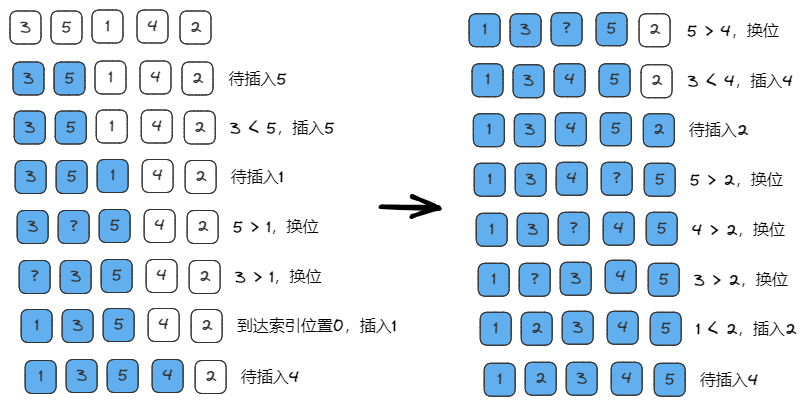
代码实现

function insertionSort(arr) {
  const { length } = arr;
  for (let i = 1; i < length; i++) {
    let j = i;
    let temp = arr[i];
    while (j >= 1 && arr[j - 1] > temp) {
      arr[j] = arr[j - 1];
      j--;
    }
    arr[j] = temp;
  }
  return arr;
}

复杂度分析

时间复杂度： $O(n^2)$。需遍历一次数组，同时遍历前面已排序的区间比较。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

4. 希尔排序

算法思想

将整个序列按照一定的间隔取值划分为若干个子序列，每个子序列分别进行插入排序，然后逐渐缩小间隔进行下一轮划分子序列和插入排序。直至最后一轮排序间隔为 1，对整个序列进行插入排序。

算法步骤

• 首先确定一个元素间隔数 gap，然后将参加排序的序列按此间隔数从第 1 个元素开始一次分成若干个子序列，即分别将所有位置相隔为 gap 的元素视为一个子序列，在各个子序列中采用某种排序方法进行排序（这里使用插入排序）；
• 然后减少间隔数，并重新将整个序列按新的间隔数分成若干个子序列，再分别对各个子序列进行排序；如此下去，直到间隔数 gap = 1。

图解思路

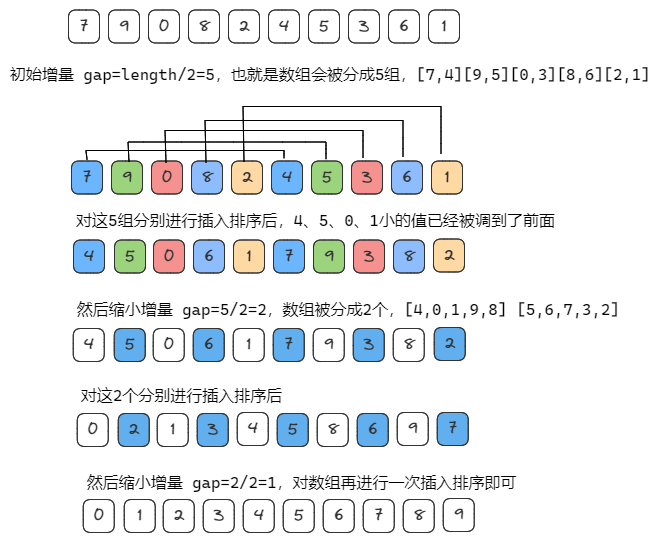
代码实现

function shellSort(arr) {
  const length = arr.length;
  let gap = Math.floor(length / 2);
  while (gap > 0) {
    // 从第gap个元素开始，逐个对其所在组进行直接插入排序操作
    for (let i = gap; i < length; i++) {
      let temp = arr[i];
      let j = i;
      while (j >= gap && arr[j - gap] > temp) {
        arr[j] = arr[j - gap];
        j -= gap;
      }
      arr[j] = temp;
    }
    gap = Math.floor(gap / 2);
  }
  return arr;
}

复杂度分析

时间复杂度：$O(nlogn)$。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

5. 归并排序

算法思想

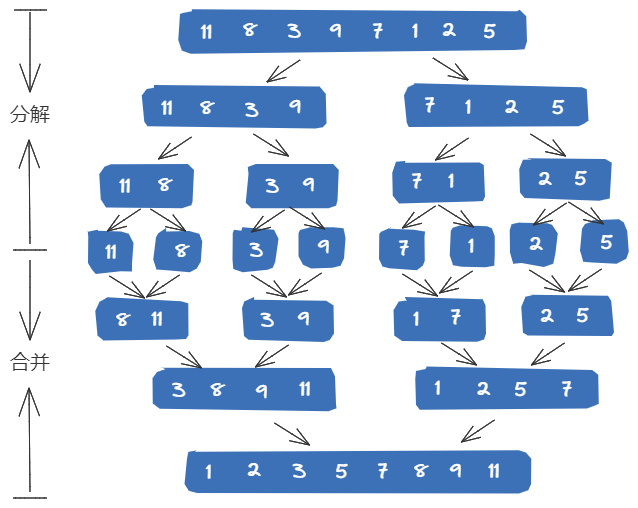
归并排序是一种分而治之算法。其思想是将原数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

算法步骤

将数组从中间分成前后两部分，然后对前后两部分分别排序，再将排序好的两部分合并在一起。

图解思路

代码实现

function merge(left, right) {
  let i = 0;
  let j = 0;
  const result = [];
  while (i < left.length && j < right.length) {
    result.push(left[i] < right[j] ? left[i++] : right[j++]);
  }
  return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}
function mergeSort(arr) {
  if (arr.length > 1) {
    const middle = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, middle));
    const right = mergeSort(arr.slice(middle));
    arr = merge(left, right);
  }
  return arr;
}

复杂度分析

时间复杂度：$O(nlogn)$。
空间复杂度：$O(n)$。

6. 快速排序

算法思想

快速排序：在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成两个部分。

算法步骤

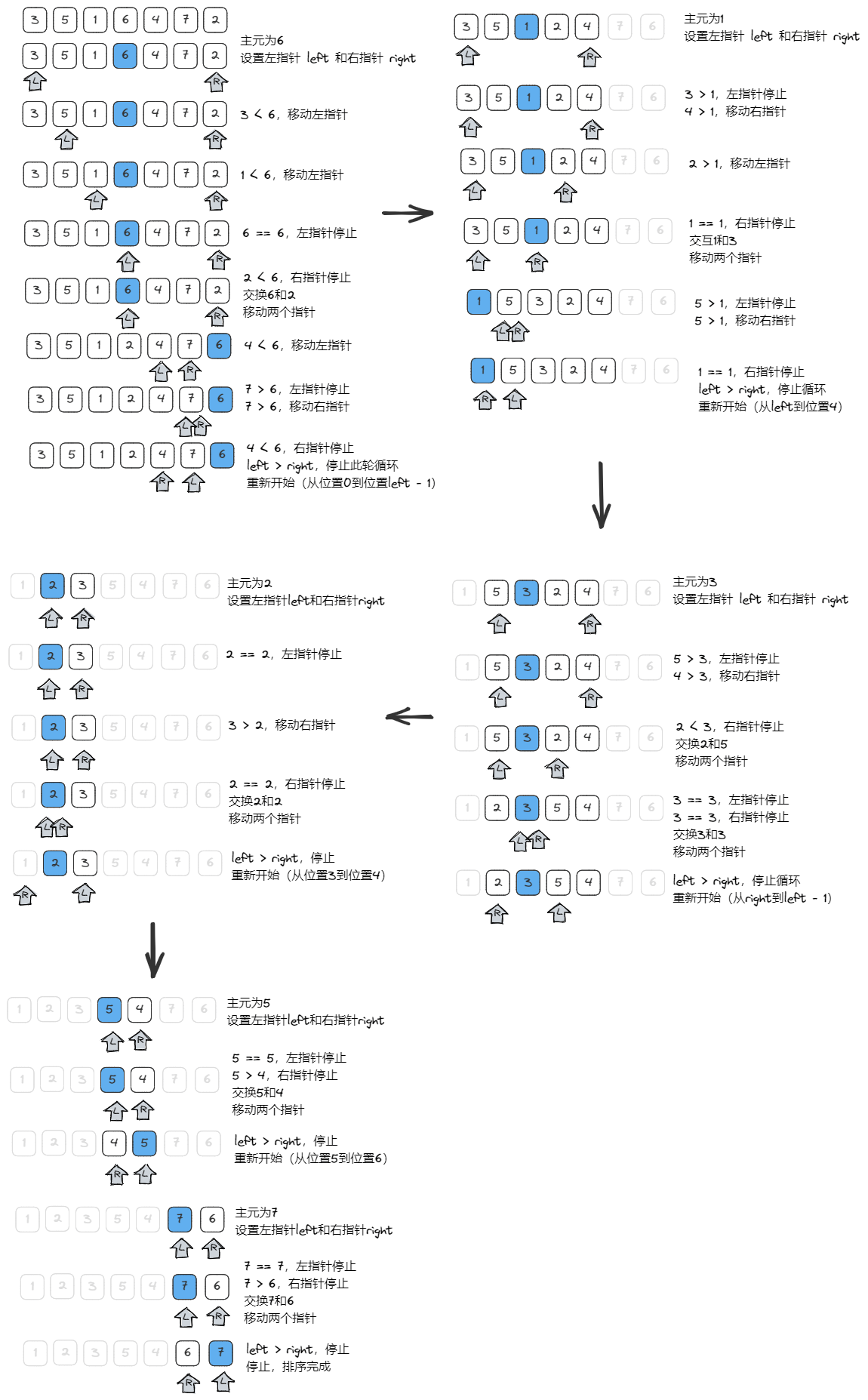
选择一个基准元素（下面选择数组的中间元素），将比它大的元素移动到右边，比它小的元素移动到左边，然后返回索引位置 i（分开左小右大的索引位置）；重复前面的步骤，直到索引位置不可再分为止（也可以说只有一个元素为止）。

图解思路

代码实现

function quickSort(arr) {
  return quick(arr, 0, arr.length - 1);
}
function quick(arr, left, right) {
  let index;
  if (array.length > 1) {
    index = partition(arr, left, right);
    if (left < index - 1) {
      quick(arr, left, index - 1);
    }
    if (index < right) {
      quick(arr, index, right);
    }
  }
}
function partition(arr, left, right) {
  const pivot = arr[Math.floor((right + left) / 2)];
  let i = left;
  let j = right;
  while (i <= j) {
    while (arr[i] < pivot) {
      i++;
    }
    while (arr[j] > pivot) {
      j--;
    }
    if (i <= j) {
      [arr[i], arr[j]] = [arr[j], arr[i]];
      i++;
      j--;
    }
  }
  return i;
}

复杂度分析

时间复杂度：$O(nlogn)$。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

7. 堆排序

算法思想

借用「堆结构」所设计的排序算法。将数组转化为大顶堆，重复从大顶堆中取出数值最大的节点，并让剩余的堆维持大顶堆性质。

算法步骤

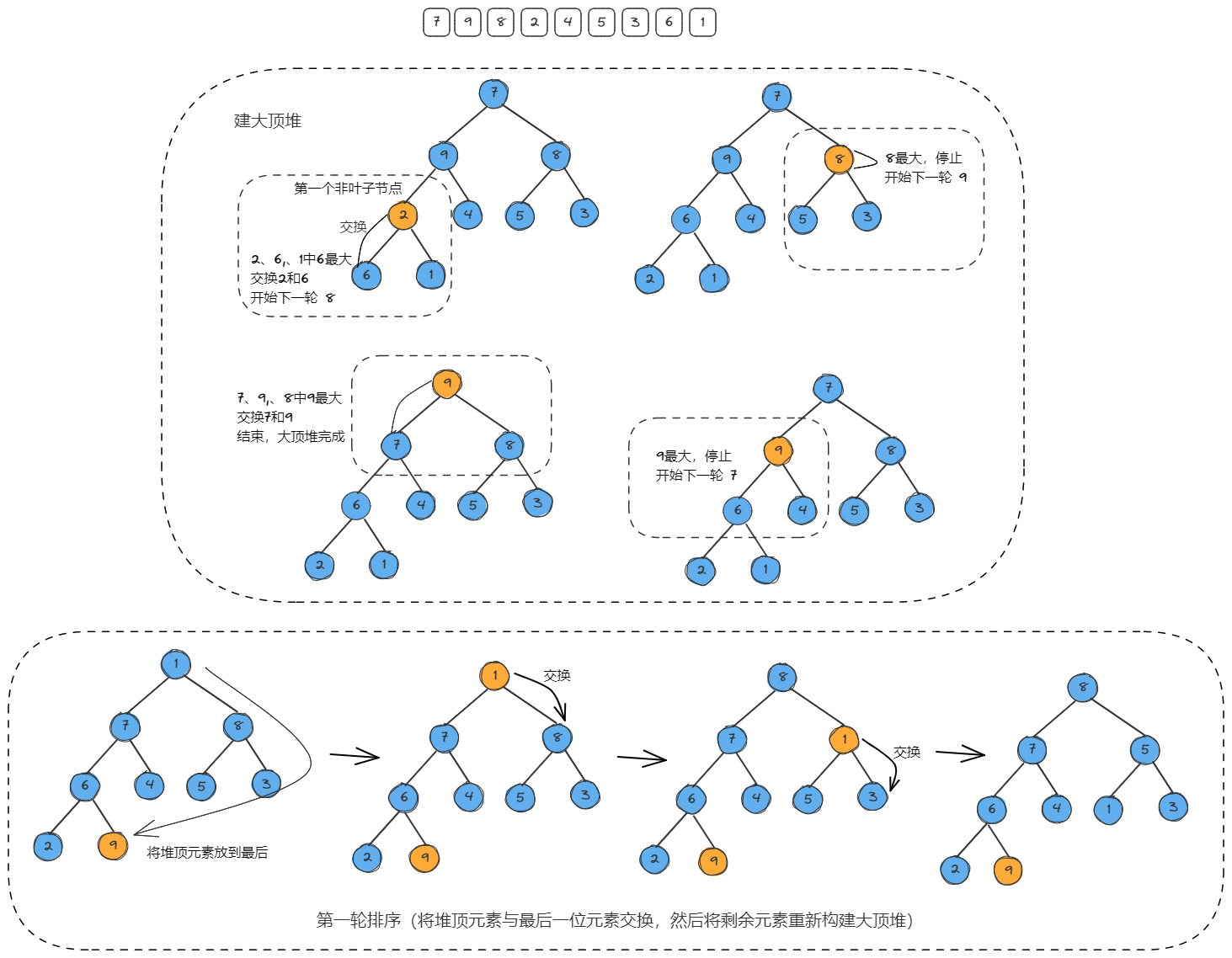
• 把无序数组构建成二叉堆，需要从小到大排序，则构建成最大堆；需要从大到小排序，则构建成最小堆；
• 循环删除堆顶元素，替换到二叉堆的末尾，调整堆产生新的堆顶。

图解思路

代码实现

function heapSort(arr) {
    buildHeap(arr, arr.length);
    let k = arr.length - 1;
    while (k > 0) {
        // 将堆顶元素放到当前堆的最后一位
        [arr[k], arr[0]] = [arr[0], arr[k]];
        k--;
        // 将未排序的元素重新构建大顶堆
        heapify(arr, k, 0);
    }
    return arr;
}
// n表示堆中元素个数
function buildHeap(arr, n) {
    //从第一个非叶子结点从下至上
    for (let i = Math.floor((n - 1) / 2); i >= 0; i--) {
        heapify(arr, n, i);
    }
}
// 堆化
function heapify(arr, n, i) {
    while (true) {
        let maxPos = i;
        // 跟左子节点比较，取最大值的位置
        if (i * 2 + 1 <= n && arr[i] < arr[i * 2 + 1]) {
            maxPos = i * 2 + 1;
        }
        // 跟右子节点比较，取最大值的位置
        if (i * 2 + 2 <= n && arr[i * 2 + 2] > arr[maxPos]) {
            maxPos = i * 2 + 2;
        }
        if (maxPos === i) {
            break;
        }
        [arr[i], arr[maxPos]] = [arr[maxPos], arr[i]];
        i = maxPos;
    }
}

复杂度分析

时间复杂度：$O(nlogn)$。
空间复杂度：$O(1)$。只需要使用常数的额外空间。

8. 计数排序

算法思想

计数排序和其他排序不一样，并不是通过比较元素的大小来实现的，而是通过统计所有相同元素出现的次数来进行排序，思路与其他的排序大有区别。

作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法步骤

• 找出待排序数组中最大值元素和最小值元素；
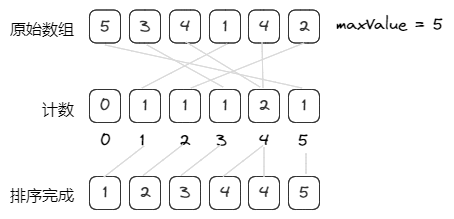
• 统计数组中每个值为 i 的元素出现的次数，存入数组的第 i 项；
• 对所有的计数累加（从 counts 中的第一个元素开始，每一项和前一项累加）
• 反向填充目标数组：将每个元素 i 放在新数组的第 counts[i] 项，每放一个元素就要将 counts[i] -= 1。

图解思路

代码实现

function countSort(arr) {
    let maxValue = arr[0];
    // 找到最大值
    for (let i = 1; i < arr.length; i++) {
        if (arr[i] > maxValue) {
            maxValue = arr[i];
        }
    }
    const temp = new Array(maxValue + 1);
    temp.fill(0);
    // 计算每个元素的个数，放入temp中
    for (let i = 0; i < arr.length; i++) {
        temp[arr[i]]++;
    }
    // // 将结果拷贝给arr数组
    let p = 0;
    for (let i = 0; i < temp.length; i++) {
        let j = temp[i];
        while (j > 0) {
            arr[p++] = i;
            j--;
        }
    }
    return arr;
}

复杂度分析

时间复杂度：$O(n)$。
空间复杂度：$O(n)$。其中n为数组中最大元素的值，需要长度为n的临时数组来计数。

9. 桶排序

算法思想

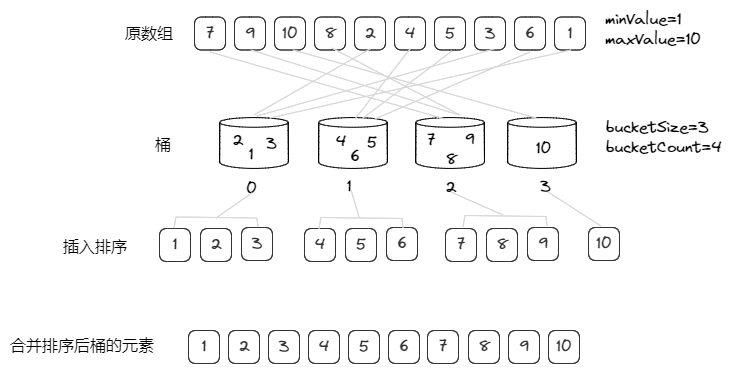
桶排序（Bucked Sort）是将待排序集合中处于同一值域的元素存入同一桶中，也就是根据元素值特性将集合拆分为多个区域，则拆分后形成的多个桶，从值域上开是处于有序状态的。对每个桶中元素进行排序，则所有桶中元素构成的集合是已排序的。

算法步骤

• 将区间划分为 n 个相同大小的子区间，每个区间称为一个桶；
• 遍历数组，将每个元素装入对应的桶中；
• 对每个桶内的元素单独排序（使用插入、归并、快排等算法）；
• 最后按照顺序将桶内的元素合并起来。

图解思路

代码实现

function bucketSort(arr) {
    if (arr.length < 2) {
        return arr;
    }
    // 创建桶
    const buckets = createBuckets(arr);
    return sortBuckets(buckets);
}
function createBuckets(arr) {
    // 每个桶中元素个数，为了方便，这里用3
    const bucketSize = 3;
    let minValue = arr[0];
    let maxValue = arr[0];
    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < minValue) {
            minValue = arr[i];
        } else if (arr[i] > maxValue) {
            maxValue = arr[i];
        }
    }
    // 桶的个数
    const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
    const buckets = [];
    for (let i = 0; i < bucketCount; i++) {
        buckets[i] = [];
    }
    for (let i = 0; i < arr.length; i++) {
        const bucketIndex = Math.floor((arr[i] - minValue) / bucketSize);
        buckets[bucketIndex].push(arr[i]);
    }
    return buckets;
}
function sortBuckets(buckets) {
    const sortedArray = [];
    for (let i = 0; i < buckets.length; i++) {
        if (buckets[i].length) {
            // 用插入排序对每个桶排序
            insertionSort(buckets[i]);
            // 将排序后的数组平铺到sortedArray中
            sortedArray.push(...buckets[i]);
        }
    }
    return sortedArray;
}

复杂度分析

时间复杂度：$O(n + k)$。其中n为数组中元素个数，k为桶个数。
空间复杂度：$O(n + k)$。其中n为数组中元素个数，k为桶个数。

10. 基数排序

算法思想

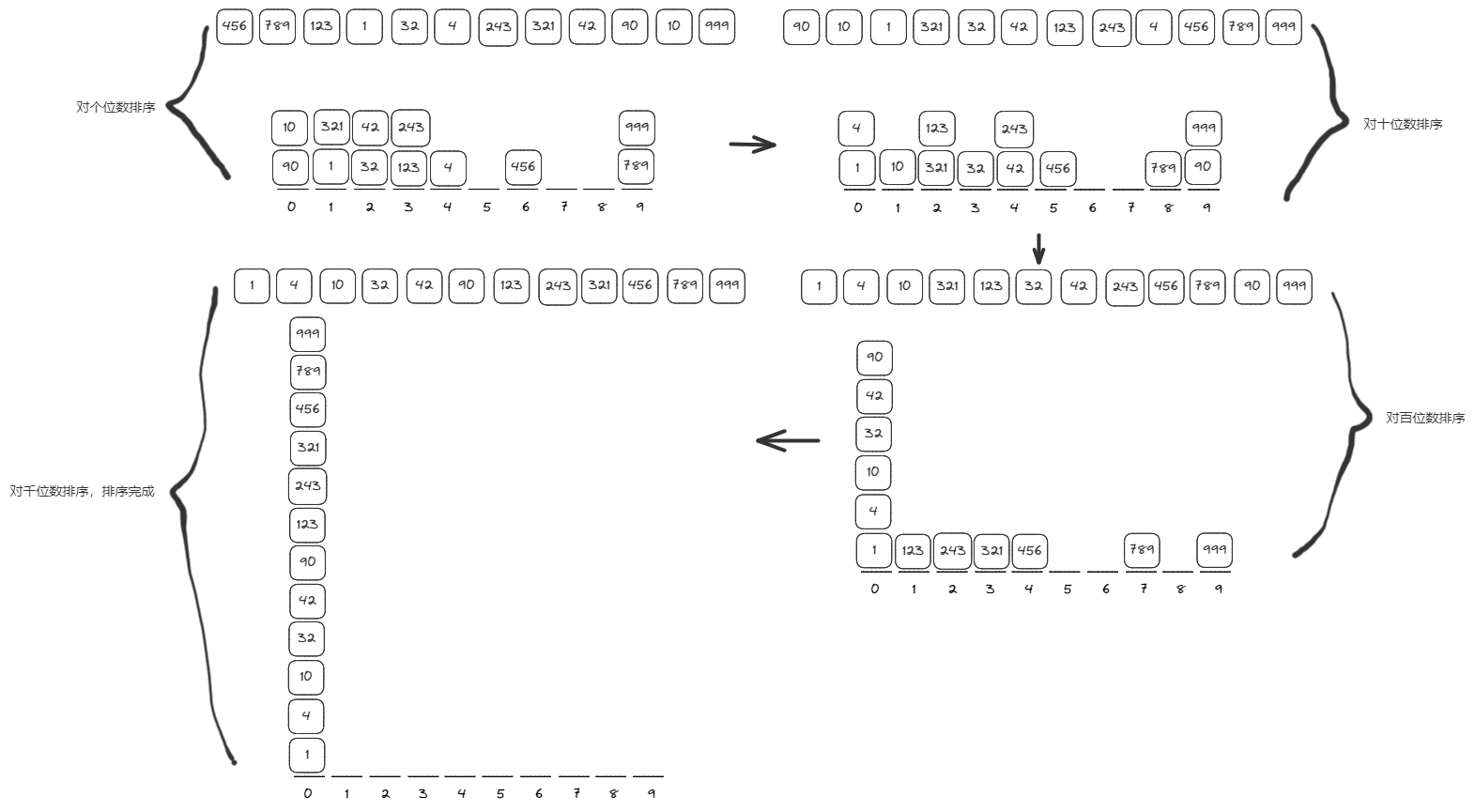
基数排序在计数排序的基础上进行了改进，将排序工作拆分为多个阶段，每一个阶段只根据一个字符进行排序，一共排序n轮(n为数据长度)。

算法步骤

基数排序会先基于最后一位有效位对数字开始排序，在下次迭代时，会基于第二个有效位进行排序，然后是第三个有效位，以此类推，直到没有待排序的有效位

图解思路

代码实现

/**
 * maxDigit {number} 最大位数
**/
function radixSort(arr, maxDigit = 10) {
    if (arr.length < 2) {
        return arr;
    }
    let mod = 10;
    // 第几位开始排序（从后往前）
    let dev = 1;
    let counter = [];
    for (let i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        // 根据有效位分配到桶（有效位相同的在一个桶）
        for (let j = 0; j < arr.length; j++) {
            // 获取当前有效位
            const bucket = Math.floor((arr[j] % mod) / dev);
            if (!counter[bucket]) {
                counter[bucket] = [];
            }
            counter[bucket].push(arr[j]);
        }
        // 如果只是一个桶中有数据，则说明排序完成
        if (counter[0].length === arr.length) {
            break;
        }
        let pos = 0;
        // 将桶中元素重新赋值给原数组（已根据有效位排序过）
        for (let j = 0; j < counter.length; j++) {
            let value;
            if (counter[j] && counter[j].length) {
                value = counter[j].shift();
                while (value >= 0) {
                    arr[pos++] = value;
                    value = counter[j].shift();
                }
            }
        }
    }
    return arr;
}

复杂度分析

时间复杂度：$O(n * k)$。其中n为数组中元素个数，k为桶个数。
空间复杂度：$O(n + k)$。其中n为数组中元素个数，k为桶个数。

能力有限，水平一般，如有错误的，欢迎指正。